Já que o meu último post foi sobre interfaces, hoje resolvi falar de uma das qualidades fundamentais
em uma interface: a conversão.

Desde os tempos dos tambores da selva ou dos sinais de fumaça, que o homem sabe a utilidade da codificação para a transmissão de informações. O código Morse, por exemplo, permitiu transmitir mensagens através de linhas sem qualidade suficiente para a transmissão de voz.
A escrita nada mais é que um código visual para a representação de palavras.
Codificar uma informação implica numa maior independência das características do meio de
armazenamento/ transmissão. Foi assim que nos livramos do chiado da fita analógica. Além disso, no caso da digitalização (e isso vale para áudio e imagem), uma vez que a informação esteja codificada, pode ser realizada uma infinidade de manipulações com os dados, destrutiva ou não-destrutivamente.
É isso o que acontece ao “ziparmos” um arquivo texto ou comprimirmos uma imagem para JPEG.
O áudio digitalizado é nada mais que uma série de números, e como tal podem ser submetidos a infinitas operações matemáticas, tornando possível obter resultados inimagináveis no campo analógico. O primeiro fator a ser subvertido é o tempo. Enquanto as operações com o áudio analógico são dependentes do tempo, digitalmente é possível por exemplo verificar instantaneamente em que ponto acontece uma virada de bateria ou um evento qualquer.
Para que tudo isto seja possível, porém, é fundamental que a codificação – a transformação das ondas elétricas do sinal de áudio em números – seja feita de maneira a preservar todas as características do sinal original.
Da qualidade da conversão dependerá a qualidade de toda a informação codificada.
Veremos a seguir como se realiza esta conversão.
OS PRINCÍPIOS DA CONVERSÃO
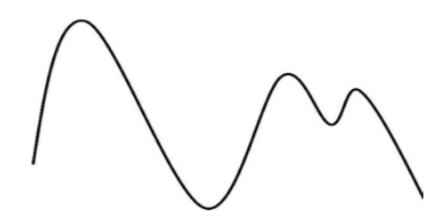
Vamos supor que desejamos copiar exatamente uma curva. (figura 1)
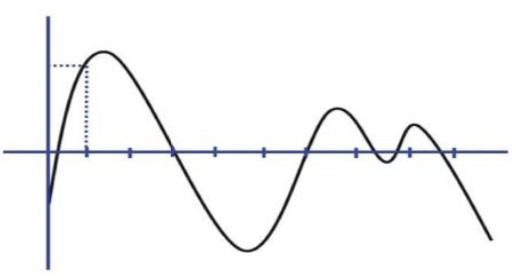
A primeira coisa que faríamos seria colocar eixos de referência. A seguir, estabeleceríamos divisões regulares no eixo horizontal e para cada divisão mediríamos a altura do ponto correspondente da curva, como mostra a figura 2.
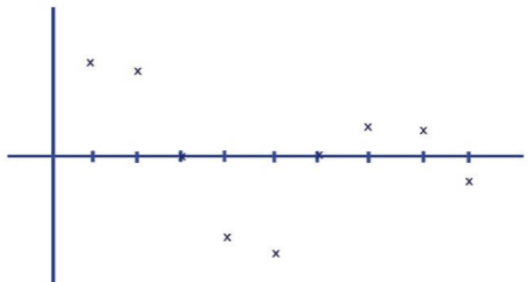
Fazendo isso para todas as divisões, teríamos o gráfico visto na figura 3.
Pode-se notar que para um número de pontos muito pequeno como este temos pouca chance de desenhar uma nova figura que se pareça suficientemente com a original. Repare que na região da extrema direita perdemos a informação de que a curva possuía uma porção negativa no trecho.
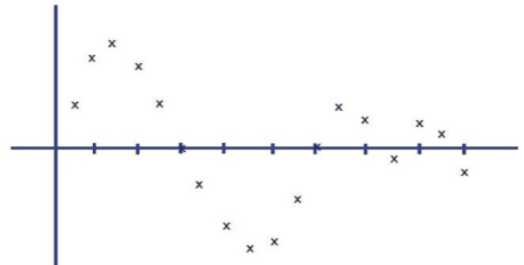
Dobrando-se o número de pontos, aproximamo-nos mais da forma de onda original, obtendo inclusive a informação
de cruzamento pelo zero na região indicada anteriormente.
TRANSPORTANDO PARA O ÁUDIO
O processo de conversão analógico/digital é mais ou menos o mesmo. Admitindo que o eixo horizontal represente tempos e o vertical amplitudes, iremos a cada intervalo pré-estabelecido proceder a uma medida da amplitude do sinal. A esta medida chamamos amostra (ou sample); ao ato de medir chamamos amostragem (sampling) e ao número de vezes que se amostra por segundo, taxa de amostragem (sampling rate).
O valor desta amplitude é convertido em um número digital para poder ser armazenado e/ou transmitido.
Mais adiante iremos conhecer como se dá a geração destes valores digitais.
Por ora, voltamos à questão da quantidade de pontos necessária para um desenho fiel da curva.
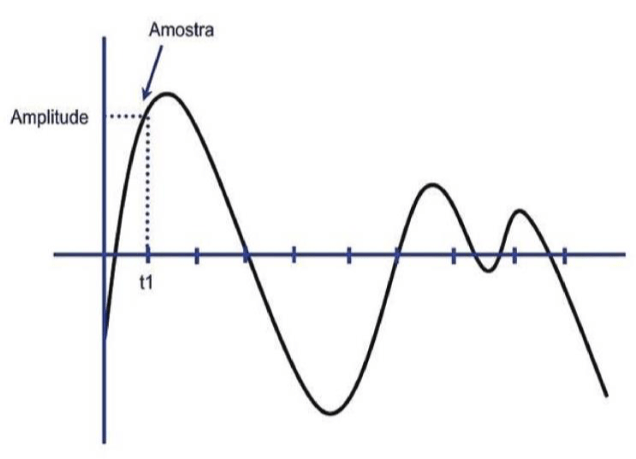
No nosso caso (figura 5), a forma da onda começou a ser mais fiel quando o número de pontos foi tal que ficou possível representar todas as sinuosidades da curva.
Será que se pode calcular o número mínimo de pontos que satisfaça esta condição?
HARMÔNICOS E SÉRIE DE FOURIER
Para isso, vamos recorrer a Fourier, que descobriu uma característica interessante das ondas periódicas (cuja forma se repete no tempo – tais como as ondas sonoras). Uma oscilação periódica de freqüência fundamental f, por mais complicada que pareça, pode ser encarada como a soma de ondas senoidais puras, com freqüências f, 2f, 3f, 4f etc…, cada uma com uma determinada amplitude.
Assim, quando se toca em um violão a nota Lá com 220 Hz, estamos gerando uma forma de onda complexa que na verdade pode ser interpretada como a soma de senóides com 220Hz, 440Hz, 660Hz etc.
É daí que vem a Série Harmônica do estudo de Música.
O TEOREMA DE NYQUIST – TAXA DE AMOSTRAGEM
Voltando agora à conversão digital, graças ao trabalho de, Nyquist (pronuncia-se “Náiqüist”) e outros, descobriu-se que se pode calcular o menor número de amostras por segundo (a menor taxa de amostragem) necessário a representar fielmente a forma de uma onda.
Para isso, temos que primeiro admitir que existe uma freqüência máxima para este sinal de áudio.
Ou seja, qualquer que seja a forma da onda, ela não poderá conter harmônicos acima de um valor fmáx.
No caso da música, admite-se que o ouvido humano não houve nada acima de 20kHz .
Assim, podemos dizer que nossa fmáx é 20kHz.
Agora, de acordo com o Teorema de Nyquist, temos que todos os harmônicos desta forma de onda serão representáveis digitalmente se usarmos uma taxa de amostragem de pelo menos o dobro de fmáx .
Para o nosso caso a taxa de amostragem deverá ser de pelo menos 40 kHz.
Isto significa que, independente da precisão dos valores das amplitudes medidos, para digitalizar música precisamos gerar pelo menos 40.000 amostras a cada segundo. Em um CD, a taxa de amostragem é padronizada em 44.100 amostras por segundo, ou 44,1kHz.
Se quisermos converter para digital a gravação de uma conversa telefônica, sabendo que os telefones só falam até 3kHz, podemos admitir com certa folga que nossa máxima freqüência é de 6kHz, e para isso poderíamos usar uma taxa de amostragem de pelo menos 12kHz, economizando bastante, pois estaremos gerando apenas um terço das amostras necessárias para a música em geral.
O TEOREMA DE NYQUIST – ALIASING
Nyquist porém faz uma ressalva importante. Não basta admitirmos que não existe áudio acima de 20kHz.
Temos que garantir que nenhuma componente acima deste valor entre no sistema, caso contrário ocorrerá o efeito chamado aliasing (pronuncia-se “êiliesin”).
“USAR A FREQÜÊNCIA DE 48kHz, PELO MENOS NOS EQUIPAMENTOS MAIS ANTIGOS, NÃO MELHORA A RESPOSTA DE AGUDOS”
Este efeito aparece na forma de uma rotação das componentes acima do limite de Nyquist em torno da freqüência máxima. Em outras palavras, uma componente em 22kHz que foi indevidamente convertida por um sistema com taxa de amostragem de 40kHz irá aparecer,
quando reconvertida para analógico, em 18kHz (o que era 2kHz acima vira 2kHz abaixo).
Da mesma forma, uma componente em 30kHz aparecerá em 10kHz, e assim por diante.
Por causa disso, todo conversor analógico/digital possui logo na entrada um poderoso filtro anti-aliasing, para impedir que freqüências acima do limite sejam convertidas erroneamente. Só que estamos precisando de um filtro para este caso que consiga deixar passar tudo até 20kHz e nada acima deste ponto.
Tal filtro, além de fisicamente impossível de construir, acabaria tendo um custo proibitivo.
Por isso, aproveitando a brecha do teorema de Nyquist, resolveu-se usar para os padrões de áudio digital freqüências de amostragem acima do limite. É por isso que o CD usa 44.100Hz. Para dar uma folga de 2kHz para que o filtro atenue suficientemente o sinal na entrada para que o aliasing seja aceitável.
E o 48kHz?
É claro que se poderia ter optado por uma freqüência bem maior (100kHz, por exemplo), garantindo um aliasing desprezível, mas as limitações do hardware da época (final dos anos setenta) não o permitiu. Esta necessidade de se ficar perto dos 40kHz implicava no uso de filtros que, embora factíveis, ainda eram extremamente caros. Preocupados com a aceitação comercial dos novos produtos, os engenheiros de então pensaram em aumentar um pouco mais esta freqüência – perdendo qualidade na conversão devido à rapidez excessiva, mas podendo usar filtros mais baratos.
Este padrão mais popular, dito consumer digital audio, usaria então a freqüência de 48kHz.
Então fica aqui o alerta aos menos avisados.
Usar a freqüência de 48kHz, pelo menos nos equipamentos mais antigos, não melhora a resposta de agudos!
O que se tem na verdade são filtros mais baratos e conversores menos precisos.
CONVERSÃO DAS AMPLITUDES
Muito bem, já sabemos quantas amostras por segundo temos que tirar de um sinal para representar todas as suas componentes de freqüência.
Agora veremos como fazer para registrar as medidas de amplitude obtidas na amostragem.
Antes de mais nada, precisamos conhecer o jeito que os computadores e sistemas digitais deram para armazenar números. Em qualquer sistema digital, todas as informações – texto, programas, imagens, sons etc – são armazenados na forma de números.
Estes números formam um conjunto de dados digitais que são interpretados da maneira conveniente.
Os circuitos que compõem os sistemas, por sua vez, são muito hábeis em lidar com condições do tipo ligado/desligado, aceso/apagado, com tensão/sem tensão. Por isso a melhor maneira de implementar fisicamente estes números para os computadores e sistemas digitais é na forma binária.
Este sistema de numeração possui apenas dois algarismos possíveis, “0” e “1”, e qualquer número pode ser escrito usando apenas eles. Na tabela vemos como escrever os números de 0 a 20.
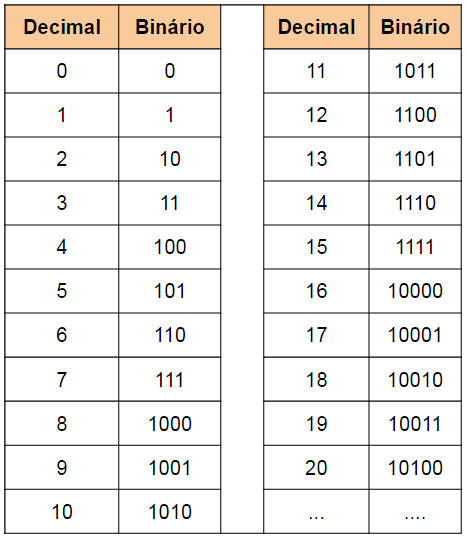
REPRESENTAÇÃO BINÁRIA
Se fôssemos escrever somente até 7, precisaríamos de apenas três dígitos. Para irmos a 15, foram necessários quatro dígitos, para 31, cinco, e assim por diante. Resumindo, com n dígitos podemos escrever 2n números diferentes.
Os conversores digitais, ao medirem a amplitude do sinal no momento da amostragem, convertem o número medido para um valor digital.
Se o conversor é “de 16 bits”, usa números de 16 dígitos binários para representar estas amplitudes.
Ora, se com 16 bits podemos escrever 216 = 65.536 números diferentes, significa que as amplitudes medidas poderão assumir apenas um destes 65.536 valores. Conversores de 24 bits permitem 16.777.216 valores possíveis.
A distância entre dois níveis consecutivos é chamada Intervalo de Quantização, ou Um Nível de Quantização.
O número de bits que compõem cada amostra determina a precisão de nossas amostras, determinando a faixa dinâmica do sinal, conforme veremos adiante.
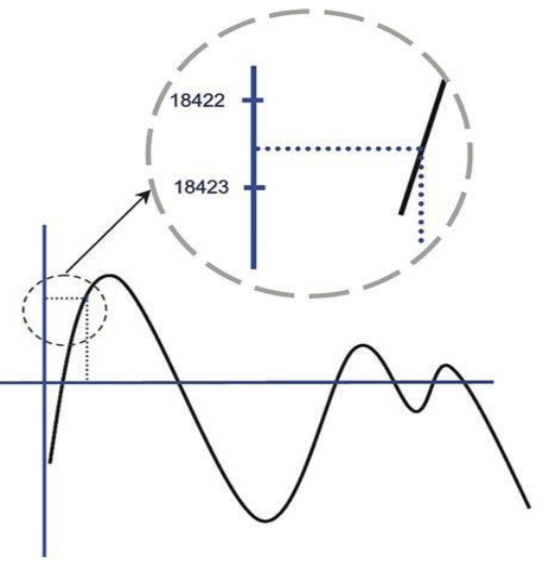
Por enquanto, vamos observar o seguinte problema. Vamos supor que estamos usando um conversor de 16 bits e que fizemos uma amostragem cuja amplitude se encontra entre os níveis 18.422 e 18.423, conforme a figura.
O conversor não conseguirá registrar exatamente o valor da amplitude, tendo que arredondá-lo para o valor possível mais próximo, neste caso o nível 18.422 de amplitude. O erro provocado por este arredondamento é chamado Erro de Quantização, e sobre ele ainda falaremos bastante.
Por enquanto basta perceber que quanto maior o número de bits por amostra usados pelo conversor,
melhor a precisão da conversão e menor o erro de quantização (figura 6).
NÚMERO DE BITS E FAIXA DINÂMICA
Agora podemos concluir que a menor amplitude detectável pelo conversor é da ordem de 1 nível de quantização.
O sinal de maior amplitude é aquele que atinge os extremos dos valores possíveis. Para calcular a relação entre o sinal de maior e o de menor amplitude, basta comparar a diferença entre estes dois níveis, o que nos dará a Faixa Dinâmica do sinal. Como já vimos acima, com 3 bits representamos 8 valores e com 4 bits, 16 valores.
De fato, para cada bit que se acrescenta, multiplicamos por dois os valores representáveis.
Estendendo um pouco o raciocínio e lembrando que dobrar a amplitude significa aumentar 6dB, temos que para cada acréscimo de 1 bit aumentamos 6 dB à faixa dinâmica. Assim, sistemas de 16bits conseguem 96dB de faixa, enquanto os de 24 bits permitem 144dB! Vale lembrar que estes valores são teóricos e não levam em conta a faixa dinâmica de todos os componentes externos – inclusive analógicos – ao conversor.
RESUMINDO…
Concluímos então que a freqüência de amostragem é responsável por garantir a resposta em freqüência do sinal convertido, enquanto que o número de bits por amostra indica a precisão das medidas e consequentemente
a faixa dinâmica do sinal.
Apêndice – Erros de Arredondamento
Como vimos, a precisão de uma medida é de extrema importância nos sistemas digitais.
Mas não é só neles que os erros de arredondamento acontecem.
Para exemplificar vamos fazer a seguinte experiência. Pegue uma calculadora e faça a seguinte conta:
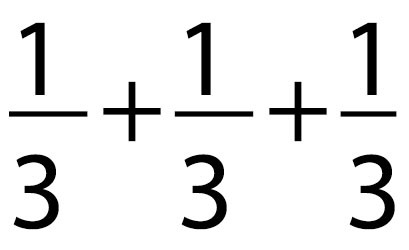
Os mais afoitos atacam vorazmente a calculadora e após algumas manipulações obtêm o brilhante resultado:
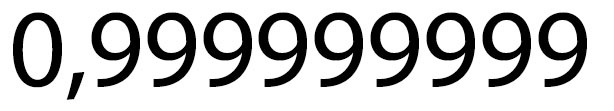
Mas quem parou um pouquinho pra pensar deixou a calculadora de lado, pois percebeu que o resultado correto é:
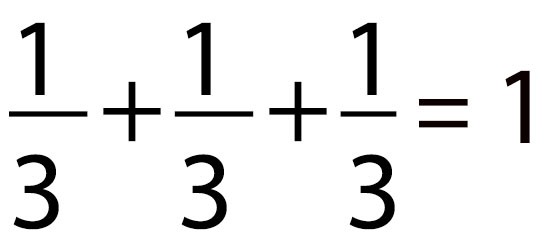
A diferença de resultados se deve à imprecisão da calculadora. Na verdade, seriam necessários infinitos dígitos à direita da vírgula para que se chegasse ao resultado correto. Esta imprecisão acontece em qualquer sistema onde se realizam operações matemáticas, e o conversor digital não poderia ser diferente.
Para um caso mais prático, tente abrir uma empresa com mais dois sócios e um capital inicial de R$ 1.000,00. Quanto caberá a cada sócio?
Quem respondeu R$ 333,33 está desprezando um centavo. O mais correto seria dizer que cada um tem “um terço de mil reais”.
Gosta dos textos do Fábio Henriques? Então você também vai gostar dos livros:
– Guia de microfonação
– Guia de Mixagem Volume 1 – Volume 2 – Volume 3
Saiba mais sobre o autor: www.fabiohenriques.com.br
Confira o curso Compressores Sem Segredos por Fábio Henriques
Acredito que você vá gostar também desse post: Faculdade de Produção Musical vale a pena?